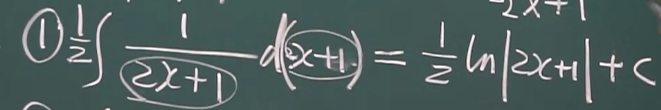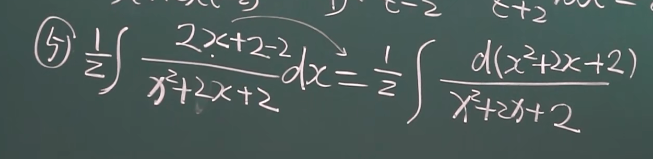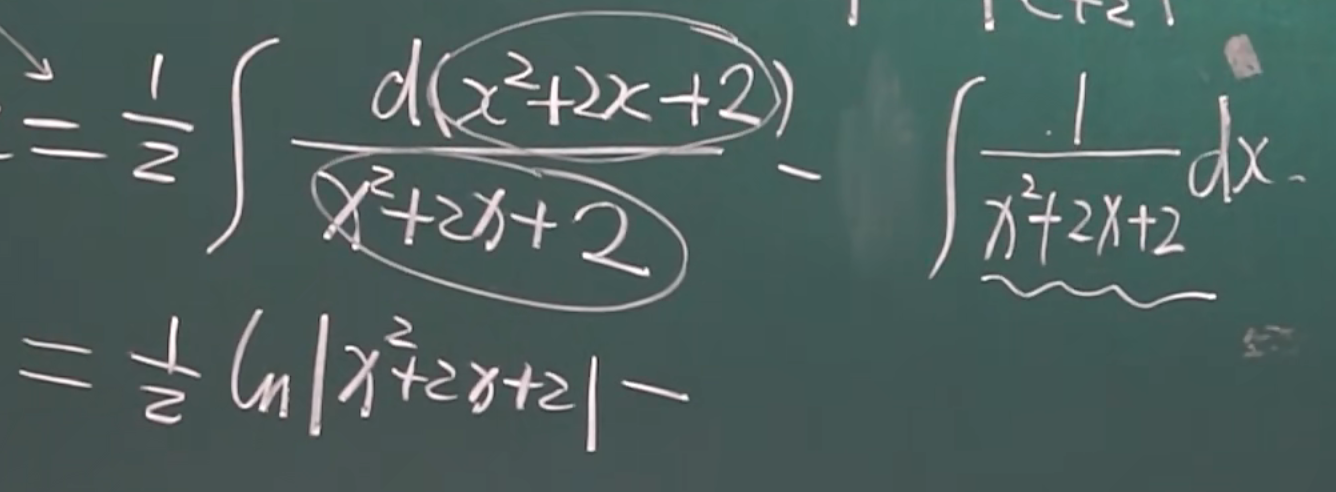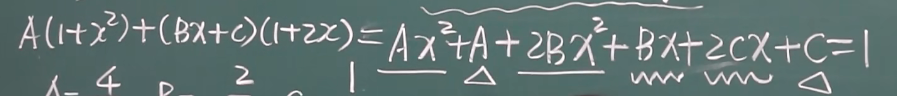不定积分.md
不定积分
定义
F’(x)=f(x) => F(x)是f(x)的一个原函数
格式如下
https://cdn.jsdelivr.net/gh/MRLOVEllletter/my-image-host@master/

原函数存在定理:连续一定有原函数()
性质
1. 与变量无关的量可以提出被积函数外
2. 只有相加相减能分开积分,相乘相除不行
第一类换元积分法(凑d)

第二类换元积分法(换元)
1. 先换元,别忘记换d里面的变量,积出来
2. 最后解出来一个形式,再换回去

分部积分法

放d的优先级
指数>三角函数>幂函数
如果把x和e^x^的优先级反过来的后果如下
出现与要求的数相同的数
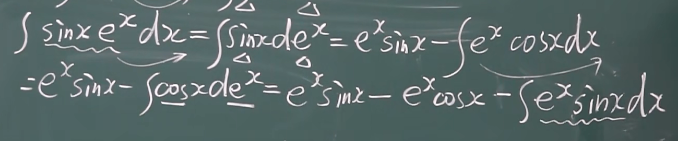
有理函数的积分
若面临这种情况

则判断m与n大小
若m大于等于n,则通过短除法使其变成 m小于n 的形式
若m小于n,则分类讨论:
分子常数,分母一次
凑ln|x|+c
分子常数,分母二次,可因式分解
式子拆成乘法拆成分式减法触发不定积分性质,凑ln绝对值
分子常数,分母二次,不可因式分解
分母配方并提常数成 关于x的平方式子加1 的形式,凑arctanu
若后面的常数不是加法而是减法,就凑出平方差从而又变为第二种
分子一次,分母二次
用第一类换元积分法消去分子的一次,d里面凑成分母
一开始是
后面要凑成
最后变成这样,就都是学过的知识了
分子常数,分母高次
用因式分解换成乘法,拆成分式加法,最后用待定系数法
待定系数法设置格式如下(一次分母设常数分子,二次分母设一次分子)
再合并分式,使分子加起来等于1,从而列出ABC的关系式方程,解方程即可
代回去,触发不定积分性质,变成前几种方法的格式了
分子二次,分母高次
因式分解换成乘法,拆成分式加法,最后用另类的待定系数法解题
待定系数法设置格式如下(涉及元素的每个次方作为分母写一遍)
神奇之处来了
式子不能拆!!!
直接代入x的不同值,从而解出ABC的值,再代回去,秒了
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 西风魔镜!
评论