定积分.md

定积分

前导

为了求曲边梯形的面积，我们在ab两点中间插入若干分点，

分成若干个小长方形（不一定间距相等）

得出：

$$
\lambda是\Delta x里面最大的那个，\xi 是区间的某一点
$$

定义

$$
f(x)在[a,b]有界，在[a,b]上任意插入分点，分成n个小区间，\Delta x_1 \Delta x_2 \Delta x_3 … \Delta x_n , 任取一点\xi _i ，
$$

则：

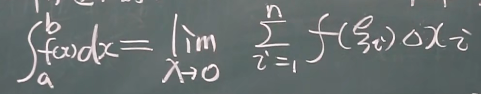
定积分只与积分区域和积分函数有关，和积分变量无关

定积分有正有负，且可抵消

性质

1. 连续必可积

2. 函数有界且是有限个间断点，那么可积

3. $$
   b=a时，\int _a ^a f(x)dx=0
   $$

4. $$
   \int _a ^b f(x)dx=-\int _b ^a f(x)dx
   $$

5. 定积分也可以拆成加法，且常数也可以提出来

6. ==基于面积加减原理，从几何能归纳出一套代数的算法，这种算法非常类似向量的加减法==

   

   推论：

   它的逻辑是：“|正数加负数| ”小于等于 “|正数|加|负数|之和”

   

7. 

   推论：

   

8. 

   推论：

   

9. 定积分中值定理：若f(x)连续，存在克赛尔属于[a,b]，使积分ab f(x)dx=f(克赛尔)(b-a)

   有：
   

   9的几何理解：

   

   相当于存在一个点构成的长方形面积与原有图形面积相等，

   这个f(克赛尔)实际上就是平均值

   5和6的图：

   

积分上限函数

定理一

函数连续必可导，导数等于被积函数（几何上每个微小的函数片段的导数都由f（t）/t算出，所以面积的导数就是函数本身）

积分上限函数为什么要把积分上限 x 和积分变量 t 用不同字母表示？它们各有什么含义？ - 小民的天空的回答 - 知乎
https://www.zhihu.com/question/264210757/answer/2240694013

积分求导上正下负

牛顿-莱布尼茨公式

best理解方式

如何简单地证明、理解牛顿-莱布尼兹公式？ - nnnnn的回答 - 知乎
https://www.zhihu.com/question/57796322/answer/352264083

分部积分法

要注意的是后面的du要提取出来变为dx，不然积分上下限就不受用了

定积分换元法

想咋换咋换，但要注意上下限，比如t=x+2，要把原有的x下和x上代入得到t下和t上

无穷限的反常积分

收敛与发散

若0到正无穷 或 负无穷到0 的积分 在t趋近于无穷时 积分的极限存在，则说这个定积分收敛

已知一个负无穷到正无穷的积分，我们将其拆成两半，若0到正无穷 和 负无穷到0 都收敛的话，那么说这个积分是无穷限的反常积分

反常积分又叫 广义积分 ，是对普通 定积分 的推广，指含有无穷上限/下限的积分

反常积分和正常积分一样求解即可